Hệ thức lượng trong tam giác vuông
Các hệ thức lượng của tam giác vuông
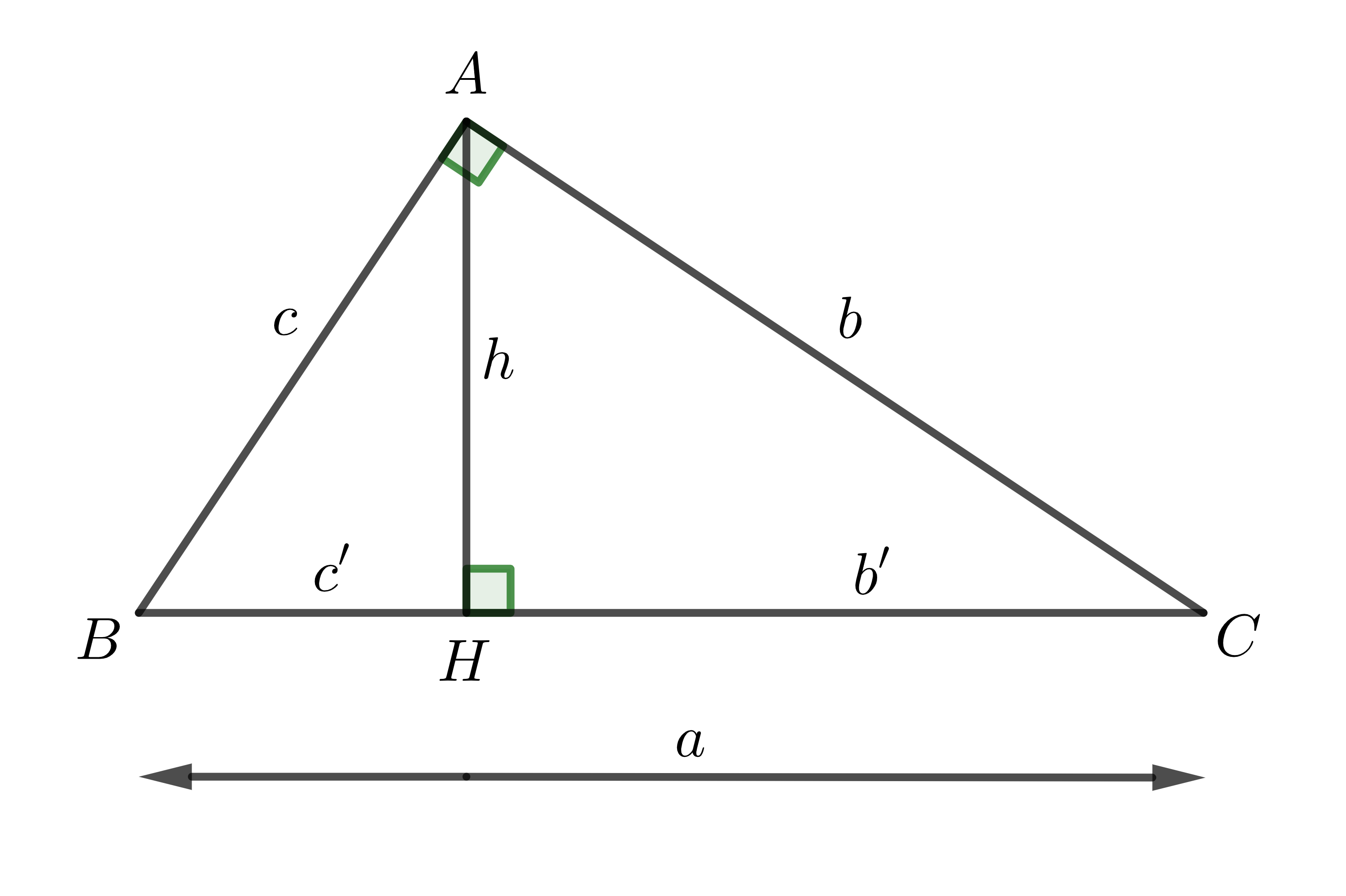
Hệ thức lượng trong tam giác vuông:
AB² = BH.BC hay c² = a.c'
AC² = CH.BC hay b² = a.b'
AH² = CH.BH hay h² = b'.c'
AB.AC = AH.BC hay b.c = a.h
AB² + AC² = BC² hay b² + c² = a²
1/ AH² = 1/AB²+ 1/AC²
Ví dụ minh họa:
Ví dụ 1: Cho tam giác ABC vuông tại A, đường cao AH vuông góc với BC. Biết AB=6, AC=8. Tính độ dài BH và CH?
Lời giải:
Áp dụng định lý Py – ta – go cho tam giác vuông ABC ta có:
AB² + AC² = BC²
⇔ 6² + 8² = BC²
⇔ BC² = 100
⇔ BC = 10
Với AH là đường cao, áp dụng hệ thức lượng cho tam giác vuông ABC ta có:
AB²= BH.BC
⇔ 6² = BH.10
⇔ 36 = BH.10
⇔ BH = 36 : 10
⇔ BH = 3,6
Tương tự ta có:
AC² = CH.BC
⇔ 8² = CH.10
⇔ 64 = CH.10
⇔ CH = 64 : 10
⇔ CH = 6,4
Ví dụ 2: Cho tam giác ABC biết độ dài các cạnh AB= 5cm, AC = 12cm, BC = 13cm, chứng minh tam giác ABC là tam giác vuông lại A.
Giải
Ta có AB² + AC²= 5²+ 12²= 25+144= 169
BC²= 13²=169
Như vậy AB²+AC²= BC²=169
=> Thỏa mãn định lý Pytago, trong tam giác vuông tổng bình phương hai cạnh góc vuông bằng bình phương cạnh huyền. Như vậy, tam giác ABC có đặc điểm là tam giác vuông tại A.
Tam giác vuông tồn tại vì nó là một kết quả trực tiếp của các nguyên tắc cơ bản của hình học Euclid và các tính chất của không gian hai chiều. Dưới đây là một số lý do và cơ sở toán học giải thích sự tồn tại của tam giác vuông:
1. Nguyên tắc Cơ bản của Hình học Euclid
Hình học Euclid, được xây dựng dựa trên năm tiên đề của Euclid, định nghĩa và mô tả các mối quan hệ giữa các điểm, đường thẳng và mặt phẳng. Một trong những tiên đề quan trọng của Euclid là:
Tiên đề 4 (góc vuông): Tất cả các góc vuông đều bằng nhau.
Dựa trên tiên đề này, chúng ta có thể xác định và xây dựng một tam giác có một góc bằng 90 độ, hay còn gọi là tam giác vuông.
2. Định lý Pythagoras
Định lý Pythagoras là một hệ quả quan trọng của hình học Euclid và nó áp dụng cho tất cả các tam giác vuông. Định lý này phát biểu rằng trong một tam giác vuông, bình phương độ dài cạnh huyền bằng tổng bình phương độ dài của hai cạnh góc vuông:
Điều này không chỉ xác định sự tồn tại của tam giác vuông mà còn cung cấp một công cụ để kiểm tra và chứng minh các tam giác vuông trong thực tế.
>> Tham khảo: Khay chống tràn dầu

Pythagoras
3. Cấu trúc Không gian Hai chiều
Trong không gian hai chiều, một góc vuông là một góc 90 độ, tạo thành khi hai đường thẳng cắt nhau vuông góc. Khi chúng ta có một góc vuông, việc kéo dài các cạnh từ đỉnh của góc vuông sẽ tạo ra một tam giác vuông. Sự tồn tại của góc vuông trong không gian hai chiều dẫn đến sự tồn tại của tam giác vuông.
4. Tính Toán và Ứng dụng Thực Tiễn
Tam giác vuông xuất hiện tự nhiên trong nhiều ứng dụng thực tiễn do các tính chất hình học của nó. Ví dụ:
Xây dựng và kiến trúc: Các kỹ sư và kiến trúc sư sử dụng các tam giác vuông để đảm bảo các góc vuông chính xác trong thiết kế và xây dựng các công trình.
Điều hướng và đo đạc: Trong điều hướng và khảo sát địa hình, các hệ thức của tam giác vuông được sử dụng để tính toán khoảng cách và vị trí.
Đồ họa và thiết kế: Trong đồ họa máy tính và thiết kế, các tam giác vuông được sử dụng để tạo ra các hình ảnh và mô hình chính xác.
5. Hình học Phẳng và Tam giác Vuông
Trong hình học phẳng, các tam giác vuông có thể được tạo ra bằng cách kết hợp các đường thẳng và góc. Ví dụ:
Tam giác vuông 3-4-5: Đây là một tam giác vuông đặc biệt với các cạnh có độ dài 3, 4 và 5 đơn vị. Sự tồn tại của tam giác này là một minh chứng cụ thể cho Định lý Pythagoras.
Tam giác vuông trong các đa giác: Tam giác vuông có thể được tìm thấy trong các đa giác phức tạp hơn, chẳng hạn như hình chữ nhật và hình vuông, nơi mỗi góc là một góc vuông.
Kết luận
Tam giác vuông tồn tại do các nguyên tắc cơ bản của hình học Euclid, tính chất của không gian hai chiều, và các ứng dụng thực tiễn trong nhiều lĩnh vực khác nhau. Tính chất đặc biệt của tam giác vuông, như Định lý Pythagoras và các tỷ số lượng giác, làm cho nó trở thành một công cụ quan trọng và không thể thiếu trong toán học và đời sống hàng ngày.
>> Xem thêm: Khối lượng các hành tinh trong hệ mặt trời
Hệ thức lượng của tam giác vuông, đặc biệt là Định lý Pythagoras, có nguồn gốc và lịch sử phong phú, bắt nguồn từ nhiều nền văn minh cổ đại. Dưới đây là một cái nhìn chi tiết về nguồn gốc và sự phát triển của các hệ thức này:
1. Ai Cập cổ đại
Người Ai Cập cổ đại đã biết đến các tính chất của tam giác vuông từ rất sớm. Họ sử dụng các tam giác với các cạnh có tỷ lệ 3:4:5 để tạo ra các góc vuông chính xác trong quá trình xây dựng các kim tự tháp và các công trình kiến trúc khác. Các phương pháp đo đạc và xây dựng này cho thấy rằng họ đã có một hiểu biết thực tế về Định lý Pythagoras, mặc dù chưa có ghi chép chính thức về một công thức toán học.
2. Lưỡng Hà cổ đại
Người Babylon cũng có kiến thức về các hệ thức trong tam giác vuông. Bằng chứng quan trọng là bảng đất sét Plimpton 322 (khoảng 1800 TCN), chứa các bộ ba số nguyên dương (còn gọi là bộ ba Pythagoras) thỏa mãn Định lý Pythagoras. Điều này cho thấy họ đã biết và sử dụng các tính chất của tam giác vuông trong các tính toán toán học và thiên văn học.
3. Ấn Độ cổ đại
Nhà toán học Ấn Độ Baudhayana (khoảng 800 TCN) đã viết trong tác phẩm "Baudhayana Sulba Sutra" về các phương pháp đo đạc và thiết kế các bàn thờ tôn giáo, trong đó bao gồm việc sử dụng các hệ thức trong tam giác vuông. Các tác phẩm của ông chứa các mô tả tương tự như Định lý Pythagoras, cho thấy rằng kiến thức về các hệ thức này đã tồn tại và được ứng dụng trong thực tiễn.
4. Trung Quốc cổ đại
Trong cuốn sách "Chu Bị Toán Kinh" (Zhou Bi Suan Jing), viết vào khoảng thế kỷ 3 TCN, có chứa các phương pháp liên quan đến Định lý Pythagoras. Cuốn sách này mô tả các cách tính toán và ứng dụng của tam giác vuông trong các hoạt động đo đạc và thiên văn học, cho thấy rằng người Trung Quốc cũng đã biết và sử dụng Định lý Pythagoras từ rất sớm.
5. Hy Lạp cổ đại
Định lý Pythagoras được đặt tên theo nhà toán học Hy Lạp Pythagoras (khoảng 570–495 TCN), người được cho là đã chứng minh định lý này. Trường phái Pythagoras đã phát triển các phương pháp chứng minh toán học cho Định lý Pythagoras và các hệ thức liên quan trong tam giác vuông. Mặc dù Định lý này đã được biết đến trước thời Pythagoras, nhưng ông và các học trò của ông đã đưa ra các chứng minh toán học chính thức.
6. Thời kỳ Trung Cổ và Phục Hưng
Nhà toán học Hồi giáo như Al-Khwarizmi và Al-Kashi đã tiếp thu và mở rộng kiến thức về các hệ thức trong tam giác vuông từ các nền văn minh trước đó. Họ đã phát triển thêm các lý thuyết và ứng dụng của tam giác vuông trong các lĩnh vực toán học và thiên văn học, và truyền bá kiến thức này sang châu u.
Trong thời kỳ Phục Hưng, kiến thức về Định lý Pythagoras và các hệ thức lượng giác được tái khám phá và mở rộng bởi các nhà toán học như Fibonacci và các nhà toán học khác.
Kết luận
Hệ thức lượng của tam giác vuông có một lịch sử lâu dài và phong phú, bắt nguồn từ nhiều nền văn minh cổ đại như Ai Cập, Babylon, Ấn Độ, Trung Quốc, và Hy Lạp. Định lý Pythagoras là một trong những định lý quan trọng nhất và được phát triển qua nhiều thế kỷ. Sự hiểu biết và ứng dụng của các hệ thức này đã đóng vai trò quan trọng trong sự phát triển của toán học và nhiều lĩnh vực khác, từ xây dựng đến thiên văn học và khoa học kỹ thuật.
Hệ thức lượng trong tam giác vuông mang lại nhiều lợi ích trong đời sống và ứng dụng trong nhiều lĩnh vực khác nhau. Dưới đây là một số lợi ích cụ thể của việc sử dụng các hệ thức này:
1. Xây dựng và Kiến trúc
Đo đạc và thiết kế chính xác: Các hệ thức lượng cho phép các kỹ sư và kiến trúc sư tính toán chính xác độ dài, chiều cao, và khoảng cách trong quá trình thiết kế và xây dựng các công trình. Ví dụ, khi xây dựng các tòa nhà, cầu, hoặc mái nhà, việc xác định các góc vuông và tính toán các cạnh theo Định lý Pythagoras là rất quan trọng.
Bảo đảm độ an toàn và bền vững: Các công trình xây dựng cần tuân thủ các tiêu chuẩn về góc và độ dốc để đảm bảo an toàn và bền vững. Các hệ thức lượng giúp đảm bảo rằng các thiết kế này đáp ứng các yêu cầu kỹ thuật.
2. Hàng không và Hàng hải
Điều hướng và định vị: Trong hàng không và hàng hải, việc xác định vị trí và điều hướng dựa vào các hệ thức lượng là rất quan trọng. Sử dụng các công cụ như sextant và GPS, các phi công và thuyền trưởng có thể xác định tọa độ và hướng di chuyển dựa trên các góc và khoảng cách.
Tính toán quỹ đạo và lộ trình: Các hệ thức lượng được sử dụng để tính toán quỹ đạo và lộ trình của máy bay và tàu thuyền, đảm bảo an toàn và hiệu quả trong việc di chuyển.
3. Thiết kế và Sản xuất
Thiết kế sản phẩm và cấu trúc: Trong ngành sản xuất, các kỹ sư sử dụng các hệ thức lượng để thiết kế các sản phẩm và cấu trúc với các góc và kích thước chính xác. Điều này đảm bảo rằng các bộ phận khớp với nhau một cách hoàn hảo trong quá trình lắp ráp.
Cải thiện hiệu suất sản xuất: Việc sử dụng các hệ thức lượng giúp tối ưu hóa quá trình sản xuất, giảm thiểu sai sót và lãng phí, từ đó cải thiện hiệu suất và chất lượng sản phẩm.
Tam giác vuông
4. Y học và Sinh học
Hình ảnh y khoa: Các hệ thức lượng được sử dụng trong việc tái tạo hình ảnh 3D từ các lát cắt 2D trong các phương pháp chụp X-quang, CT scan và MRI. Điều này giúp các bác sĩ chẩn đoán và điều trị bệnh chính xác hơn.
Nghiên cứu và phân tích cấu trúc sinh học: Các nhà khoa học sử dụng các hệ thức lượng để phân tích hình dạng và kích thước của các cấu trúc sinh học, từ cấp độ tế bào đến cơ thể động vật, giúp hiểu rõ hơn về cơ thể sống và các quá trình sinh học.
5. Giáo dục và Đào tạo
Cơ sở toán học cơ bản: Hệ thức lượng trong tam giác vuông là một phần quan trọng trong chương trình giảng dạy toán học cơ bản. Chúng giúp học sinh hiểu các khái niệm về góc, cạnh và mối quan hệ giữa chúng, từ đó xây dựng nền tảng cho các kiến thức toán học phức tạp hơn.
Phát triển kỹ năng tư duy logic: Việc học và áp dụng các hệ thức lượng giúp học sinh phát triển kỹ năng tư duy logic và giải quyết vấn đề, điều này rất quan trọng trong nhiều lĩnh vực khác nhau.
6. Ứng dụng trong Đời sống Hàng ngày
Đo đạc và sửa chữa nhà cửa: Khi cần đo đạc hoặc sửa chữa trong nhà, như xác định kích thước của một phòng hoặc lắp đặt các vật dụng, các hệ thức lượng có thể giúp tính toán chính xác mà không cần phải đo trực tiếp.
Lập kế hoạch và thực hiện các dự án DIY: Những người làm các dự án DIY (Do It Yourself) có thể sử dụng các hệ thức lượng để thiết kế và thực hiện các dự án một cách chính xác và hiệu quả hơn.
7. Thể thao và Giải trí
Phân tích kỹ thuật trong thể thao: Trong các môn thể thao như bóng rổ, golf, và bóng đá, các vận động viên và huấn luyện viên sử dụng các hệ thức lượng để phân tích kỹ thuật và cải thiện hiệu suất. Ví dụ, tính toán góc và lực cần thiết để thực hiện một cú đánh golf hoặc một cú ném bóng rổ.
Thiết kế trò chơi điện tử và đồ họa máy tính: Trong lĩnh vực trò chơi điện tử và đồ họa máy tính, các nhà phát triển sử dụng các hệ thức lượng để tạo ra các hình ảnh và hiệu ứng 3D chính xác.
Kết luận
Các hệ thức lượng trong tam giác vuông không chỉ là các công cụ toán học cơ bản mà còn có nhiều ứng dụng thực tiễn quan trọng trong đời sống và nhiều lĩnh vực khác nhau. Chúng giúp chúng ta thực hiện các phép tính đo đạc chính xác, thiết kế và xây dựng các công trình, điều hướng và định vị, cải thiện hiệu suất sản xuất, và nhiều ứng dụng khác, từ đó nâng cao chất lượng cuộc sống và hiệu quả làm việc.