Công thức tính diện tích hình tròn
Sự ra đời của hình tròn, công thức tính diện tích hình tròn cũng như nhiều khái niệm hình học khác, có nguồn gốc từ thời cổ đại và gắn liền với sự phát triển của toán học và khoa học. Dưới đây là một tóm tắt về quá trình ra đời và phát triển của hình tròn:
Thời kỳ tiền sử và cổ đại:
Hình tròn là một trong những hình dạng đầu tiên được loài người nhận biết và sử dụng trong cuộc sống hàng ngày. Người tiền sử đã quan sát các hình dạng tự nhiên như mặt trời, mặt trăng, và các ao hồ có dạng tròn.
Trong các nền văn minh cổ đại như Ai Cập, Mesopotamia, Hy Lạp, và Ấn Độ, hình tròn được sử dụng trong kiến trúc, nghệ thuật, và tôn giáo. Người Ai Cập cổ đại đã sử dụng hình tròn để xây dựng các kim tự tháp và vòng tròn đá.
Toán học cổ đại:
Người Hy Lạp cổ đại, đặc biệt là nhà toán học Euclid, đã nghiên cứu sâu về hình tròn và các tính chất của nó. Trong tác phẩm "Các yếu tố" (Elements), Euclid đã đưa ra nhiều định lý quan trọng về hình tròn.
Archimedes, một nhà toán học Hy Lạp khác, đã phát triển các phương pháp để tính diện tích và chu vi của hình tròn. Ông cũng đưa ra một ước lượng chính xác cho số π (pi).
>> Xem thêm: Hệ thức lượng trong tam giác vuông
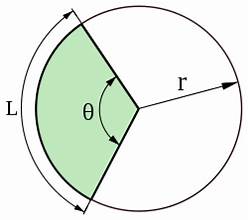
Diện tích hình tròn
Thời kỳ Trung cổ và Phục hưng:
Trong thời kỳ Trung cổ, các nhà toán học Hồi giáo như Al-Khwarizmi và Omar Khayyam đã tiếp tục nghiên cứu về hình học và hình tròn. Họ đã truyền bá và phát triển các công trình của các nhà toán học Hy Lạp.
Thời kỳ Phục hưng chứng kiến sự tái sinh của khoa học và toán học ở châu u. Các nhà toán học như Leonardo da Vinci và Johannes Kepler đã sử dụng hình tròn trong các nghiên cứu của mình về thiên văn học và cơ học.
Toán học hiện đại:
Với sự phát triển của giải tích và hình học giải tích, hình tròn trở thành một đối tượng nghiên cứu quan trọng trong toán học hiện đại. Các công trình của René Descartes và Isaac Newton đã mở ra những hướng đi mới cho việc nghiên cứu hình học và động lực học.
Hình tròn cũng đóng vai trò quan trọng trong nhiều lĩnh vực khác của khoa học và kỹ thuật, từ vật lý đến thiết kế cơ khí.
Như vậy, hình tròn không chỉ là một khái niệm hình học cơ bản mà còn là một phần không thể thiếu của sự phát triển khoa học và văn minh nhân loại. Sự nghiên cứu và hiểu biết về hình tròn đã đóng góp to lớn vào nhiều lĩnh vực khác nhau trong cuộc sống.
Công thức
Diện tích của hình tròn, như một khái niệm toán học và ứng dụng thực tiễn, mang lại nhiều lợi ích quan trọng trong đời sống. Dưới đây là một số ví dụ cụ thể về lợi ích này:
Kiến trúc và xây dựng:
Thiết kế các công trình kiến trúc: Diện tích hình tròn thường được sử dụng trong thiết kế các công trình như đài phun nước, sân vận động, nhà hát, và các công trình tôn giáo như nhà thờ và đền chùa. Hình tròn giúp tối ưu hóa không gian và tạo ra các cấu trúc thẩm mỹ, đối xứng.
Tính toán diện tích mái vòm và cầu: Trong xây dựng, việc tính toán diện tích mái vòm hay cầu tròn rất quan trọng để đảm bảo độ an toàn và hiệu quả sử dụng vật liệu.
Giao thông và quy hoạch đô thị:
Vòng xuyến giao thông: Vòng xuyến giao thông (rotary hoặc roundabout) được thiết kế theo hình tròn giúp lưu thông giao thông hiệu quả hơn, giảm tai nạn và tắc nghẽn.
Quy hoạch công viên và khu vui chơi: Các khu vực công cộng như công viên thường có các khu vực hình tròn, chẳng hạn như sân chơi hoặc khu vực tổ chức sự kiện, để tạo ra không gian mở và thu hút mọi người.
Công nghiệp và sản xuất:
Thiết kế và sản xuất các bộ phận cơ khí: Nhiều bộ phận cơ khí, như bánh răng, vòng bi, và các bộ phận quay, được thiết kế dựa trên hình tròn để đảm bảo chuyển động mượt mà và hiệu quả.
Tính toán diện tích bề mặt: Trong công nghiệp, việc tính toán diện tích bề mặt của các vật thể hình tròn giúp xác định lượng vật liệu cần thiết và tối ưu hóa quá trình sản xuất.
Nông nghiệp và thủy lợi:
Tưới tiêu hình tròn: Hệ thống tưới tiêu hình tròn (pivot irrigation) là một phương pháp tưới tiêu hiệu quả, giúp phân phối nước đều đặn và tiết kiệm nước.
Thiết kế hồ chứa nước: Hồ chứa nước hình tròn thường được thiết kế để tối ưu hóa diện tích mặt nước và giảm thiểu mất nước do bốc hơi.
Ứng dụng trong cuộc sống hàng ngày:
Bánh và pizza: Việc tính toán diện tích bánh hoặc pizza giúp chia đều phần ăn và đảm bảo tính thẩm mỹ khi cắt.
Trang trí và nghệ thuật: Trong nghệ thuật và thiết kế nội thất, hình tròn thường được sử dụng để tạo ra các họa tiết và vật trang trí đẹp mắt, cân đối.
Khoa học và giáo dục:
Thiên văn học: Diện tích hình tròn đóng vai trò quan trọng trong việc tính toán kích thước và quỹ đạo của các hành tinh, ngôi sao, và các thiên thể khác.
Giáo dục toán học: Việc giảng dạy về diện tích hình tròn giúp học sinh hiểu rõ hơn về hình học và các khái niệm liên quan, từ đó phát triển tư duy logic và khả năng giải quyết vấn đề.
Tóm lại, diện tích của hình tròn không chỉ là một khái niệm toán học quan trọng mà còn có nhiều ứng dụng thực tiễn trong nhiều lĩnh vực khác nhau của đời sống, từ kiến trúc, giao thông, công nghiệp, nông nghiệp, cho đến khoa học và giáo dục.
Hình tròn là một trong những hình dạng cơ bản và phổ biến nhất trong tự nhiên và cuộc sống hàng ngày, mang lại nhiều lợi ích và ứng dụng quan trọng. Dưới đây là một số lý do tại sao hình tròn lại cần thiết và được ưa chuộng:
Tính đối xứng và thẩm mỹ:
Đối xứng hoàn hảo: Hình tròn có tính đối xứng hoàn hảo, tạo cảm giác cân đối và hài hòa. Điều này làm cho hình tròn trở thành lựa chọn lý tưởng trong thiết kế kiến trúc, nghệ thuật và trang trí.
Thẩm mỹ: Các vật thể hình tròn thường được coi là đẹp mắt và hấp dẫn, góp phần tạo nên không gian sống và làm việc dễ chịu.
Ứng dụng trong khoa học và kỹ thuật:
Thiên văn học: Hình tròn và các vòng tròn đồng tâm được sử dụng để mô tả quỹ đạo của các hành tinh và các thiên thể khác, giúp các nhà thiên văn học hiểu rõ hơn về vũ trụ.
Cơ học: Nhiều bộ phận cơ khí, như bánh xe, vòng bi, và bánh răng, đều có dạng hình tròn để đảm bảo chuyển động mượt mà và hiệu quả.
Hiệu quả trong thiết kế và sử dụng không gian:
Tối ưu hóa không gian: Hình tròn giúp tối ưu hóa diện tích sử dụng trong nhiều trường hợp, chẳng hạn như các vòng xuyến giao thông, sân vận động, và các công trình công cộng khác.
Phân phối lực đều: Các công trình kiến trúc như mái vòm và cầu tròn có thể phân phối lực đều đặn, tăng độ bền và độ an toàn.
Ứng dụng trong công nghiệp và sản xuất:
Dễ dàng gia công: Các vật thể hình tròn dễ gia công và sản xuất hàng loạt, giảm chi phí và thời gian sản xuất.
Hiệu suất cao: Trong nhiều máy móc và thiết bị, các bộ phận hình tròn giúp tăng hiệu suất và độ chính xác trong vận hành.
Ứng dụng trong cuộc sống hàng ngày:
Đồ dùng và nội thất: Nhiều đồ dùng hàng ngày, như bàn, ghế, đồng hồ, và gương, có hình tròn vì tính thẩm mỹ và tiện dụng.
Diện tích toàn phần hình trụ
Thực phẩm: Hình tròn thường được sử dụng trong chế biến thực phẩm, như bánh pizza, bánh quy, và đĩa ăn, để dễ dàng chia sẻ và phục vụ.
Tính chất toán học và giáo dục:
Dễ hiểu và dễ giảng dạy: Hình tròn có các tính chất toán học đơn giản nhưng sâu sắc, dễ hiểu và dễ giảng dạy cho học sinh, giúp họ phát triển tư duy logic và kỹ năng giải quyết vấn đề.
Cơ sở cho nhiều khái niệm khác: Nhiều khái niệm toán học và hình học phức tạp hơn dựa trên hình tròn, như số pi (π), diện tích và chu vi hình tròn, và các phép biến hình.
Hiện diện trong tự nhiên:
Các hiện tượng tự nhiên: Hình tròn xuất hiện tự nhiên trong nhiều hiện tượng và đối tượng tự nhiên, như mặt trời, mặt trăng, giọt nước, và các vòng tròn đồng tâm trong hồ nước khi có vật rơi vào.
Tóm lại, hình tròn có mặt trong rất nhiều lĩnh vực và khía cạnh của cuộc sống, từ khoa học, kỹ thuật, kiến trúc, đến cuộc sống hàng ngày và giáo dục. Sự phổ biến và cần thiết của hình tròn xuất phát từ tính đối xứng, tính thẩm mỹ, và những ứng dụng thực tiễn đa dạng của nó.