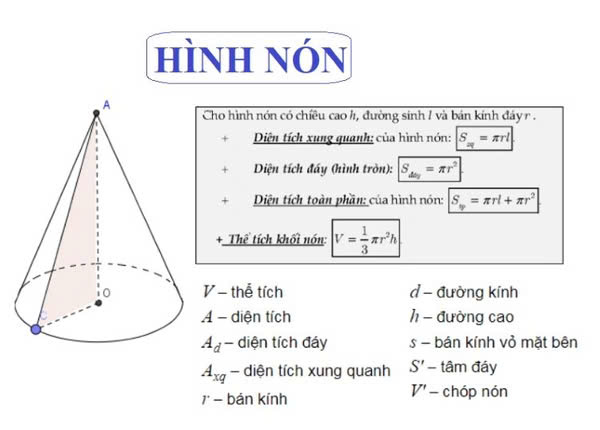
Diện tích xung quanh hình nón
Hình nón là một khối hình học ba chiều, nổi bật với đặc điểm có một đáy hình tròn và một đỉnh (hay còn gọi là đỉnh nón). Đáy và đỉnh được kết nối với nhau bằng các đường sinh, tạo thành bề mặt cong. Dưới đây là một số đặc điểm và thông tin chi tiết về hình nón:
Đặc điểm của hình nón:
- Đáy: Hình nón có một đáy hình tròn.
- Đỉnh: Hình nón có một đỉnh đơn lẻ, nằm trên đáy.
- Đường sinh: Các đoạn thẳng nối từ đỉnh đến các điểm trên đường tròn của đáy được gọi là đường sinh.
- Chiều cao: Chiều cao của hình nón là khoảng cách từ đỉnh đến đáy, vuông góc với mặt đáy.
- Bán kính: Bán kính là bán kính của đáy hình tròn.

Công thức tính diện tích hình nónDiện tích xung quanh của hình nón (hay còn gọi là diện tích mặt ngoài của hình nón) được tính bằng công thức:
S xq = π r l
Trong đó:
- S xq: diện tích xung quanh của hình nón.
- r: bán kính đáy của hình nón.
- l: độ dài đường sinh của hình nón.
Trong hình nón, có một số đơn vị đo lường và ký hiệu quan trọng mà bạn cần biết để xác định các thuộc tính của nó.
Đơn vị đo lường
- Chiều cao (h): Đo chiều cao từ đáy đến đỉnh của hình nón. Thông thường, đơn vị đo là cm (centimeter) hoặc m (meter).
- Bán kính (r): Đo bán kính của đáy hình tròn. Ký hiệu là r. Đơn vị đo cũng có thể là cm hoặc m.
- Đường sinh (l): Đo độ dài từ đỉnh đến điểm trên đường tròn đáy. Ký hiệu là l. Đơn vị đo là cm hoặc m.
- Diện tích xung quanh (S xq): Đo diện tích bề mặt bên ngoài của hình nón. Ký hiệu là S xq. Đơn vị đo là cm² hoặc m².
- Diện tích đáy (S đáy): Đo diện tích mặt đáy của hình nón. Ký hiệu là S đáy. Đơn vị đo là cm² hoặc m².
- Diện tích toàn phần (S tp): Đo tổng diện tích bao gồm cả diện tích xung quanh và diện tích đáy. Ký hiệu là S tp. Đơn vị đo là cm² hoặc m².
- Thể tích (V): Đo không gian bên trong hình nón. Ký hiệu là V. Đơn vị đo là cm³ hoặc m³.
Ký hiệu và công thức
- Diện tích xung quanh: Sxq = π rl
- Diện tích đáy: Sđáy = π r²
- Diện tích toàn phần: Stp = Sxq + Sđáy = π rl + π r² = π r (l + r)
- Thể tích: V = (1/3) π r² h
Ví dụ về đơn vị đo
- Nếu bán kính của đáy hình nón là 3 cm, chiều cao là 4 cm, và độ dài đường sinh là 5 cm, thì:
- Bán kính (r) = 3 cm
- Chiều cao (h) = 4 cm
- Đường sinh (l) = 5 cm
Những ví dụ về diện tích hình nónDưới đây là một số ví dụ thực tế và bài toán minh họa liên quan đến diện tích xung quanh của hình nón:
Ví dụ 1: Nón bảo hiểm
- Mô tả: Một nón bảo hiểm có bán kính đáy là 10 cm và độ dài đường sinh là 25 cm.
- Cách tính: Diện tích xung quanh Sxq = π r l = π × 10 × 25 ≈ 785.4 cm²
Ví dụ 2: Ly kem
- Mô tả: Một ly kem hình nón có bán kính đáy là 4 cm và độ dài đường sinh là 10 cm.
- Cách tính: Diện tích xung quanh Sxq = π r l = π × 4 × 10 ≈ 125.66 cm².
Ví dụ 3: Tháp chuông
- Mô tả: Một tháp chuông hình nón có bán kính đáy là 6 m và độ dài đường sinh là 8 m.
- Cách tính: Diện tích xung quanh Sxq = π r l = π × 6 × 8 ≈ 150.8 m².
Ví dụ 4: Mái nhà hình nón
- Mô tả: Một mái nhà hình nón có bán kính đáy 5 m và chiều dài đường sinh là 7 m.
- Cách tính: Diện tích xung quanh Sxq = π r l = π × 5 × 7 ≈ 109.96 m².
Ví dụ 5: Bánh sinh nhật hình nón
- Mô tả: Một chiếc bánh sinh nhật có hình dạng nón với bán kính đáy là 8 cm và độ dài đường sinh là 12 cm.
- Cách tính: Diện tích xung quanh Sxq = π r l = π × 8 × 12 ≈ 301.59 cm².
Ví dụ 6: Thùng chứa hình nón
- Mô tả: Một thùng chứa có hình nón với bán kính đáy là 3 m và chiều dài đường sinh là 5 m.
- Cách tính: Diện tích xung quanh Sxq = π r l = π × 3 × 5 ≈ 47.12 m².
Những ví dụ trên giúp bạn hình dung rõ hơn về diện tích xung quanh của hình nón trong thực tế.
Những ứng dụng của hình nónHình nón là một khối hình học phổ biến và có nhiều ứng dụng trong đời sống và các lĩnh vực khác nhau. Dưới đây là một số ứng dụng điển hình của hình nón:
Kiến trúc và xây dựng
- Mái vòm: Hình nón thường được sử dụng trong thiết kế mái vòm của các nhà thờ, đền, và các công trình kiến trúc khác. Hình dáng của nó không chỉ đẹp mà còn giúp nước mưa dễ dàng chảy xuống, giảm thiểu sự tích tụ trên mái.
- Tháp: Nhiều tháp cao và chóp đều có hình nón, chẳng hạn như tháp Eiffel ở Paris.
Công nghiệp
- Thùng chứa: Nhiều loại thùng chứa, như thùng đựng thực phẩm hoặc hóa chất, được thiết kế theo hình nón để tiết kiệm không gian và thuận tiện trong việc xếp chồng.
- Nón bảo hiểm: Hình nón được sử dụng trong thiết kế nón bảo hiểm để bảo vệ đầu người dùng, giúp phân tán lực tác động khi có va chạm.
Thực phẩm
- Bánh kem: Nhiều loại bánh kem có hình nón, mang lại vẻ đẹp và hấp dẫn cho món ăn.
- Ly kem: Ly kem hình nón là một ví dụ điển hình trong ngành công nghiệp thực phẩm, thường được sử dụng để đựng kem và các loại đồ ăn nhẹ.
Giao thông
- Biển báo giao thông: Một số biển báo giao thông, như biển báo cấm hoặc cảnh báo, có hình nón để nổi bật và dễ nhận diện.
- Cột đèn giao thông: Cột đèn giao thông đôi khi có hình nón để tạo sự chú ý cho người tham gia giao thông.
Khoa học và giáo dục
- Mô hình hình học: Hình nón thường được sử dụng trong các bài học về hình học để giúp học sinh hiểu rõ về các khái niệm như diện tích, thể tích và các tính chất của hình học không gian.
- Vật lý: Trong các thí nghiệm vật lý, hình nón có thể được sử dụng để mô phỏng các hiện tượng như chuyển động của dòng chảy, hoặc mô hình hóa các trường hợp trong quang học.
Nghệ thuật và thiết kế
- Điêu khắc: Nhiều tác phẩm nghệ thuật và điêu khắc sử dụng hình nón như một phần trong thiết kế của chúng.
- Thiết kế đồ họa: Hình nón thường được sử dụng trong thiết kế đồ họa, hoạt hình và trò chơi để tạo ra các hình khối 3D.
Thiên văn học
- Hình nón ánh sáng: Trong nghiên cứu ánh sáng và hình học, hình nón có thể được dùng để mô phỏng các chùm sáng và hướng sáng trong không gian.
- Trên đây là các công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của hình nón. Hy vọng bài viết sẽ mang lại lợi ích lớn trong học tập và công việc cho bạn.
Ngoài ra, nếu bạn có nhu cầu về các thiết bị rửa mắt khẩn cấp chính hãng, chất lượng tốt hãy liên hệ với chúng tôi để được tư vấn chi tiết nhé!
Thông tin chi tiết, vui lòng liên hệ:
CÔNG TY TNHH THƯƠNG MẠI DỊCH VỤ L M QUANG PHÁT
Địa chỉ: 33/20 Bến Lội, phường Bình Trị Đông A, quận Bình Tân, TP HCM
Hotline: 0931.816.846
Email: itquangtran88@gmail.com
|