Hệ thức lượng trong tam giác vuông
Hệ thức lượng trong tam giác vuông là tập hợp các quy tắc và công thức được áp dụng vào tam giác có một góc vuông (90 độ). Các công thức này rất hữu ích trong việc tính toán các đại lượng như độ dài các cạnh, diện tích, chu vi và các mối liên hệ giữa các góc và cạnh của tam giác vuông. Dưới đây là một số hệ thức lượng trong tam giác vuông cơ bản:
Định lý Pythagore (Pythagoras' Theorem):
Định lý Pythagore là một trong những công thức quan trọng nhất trong hệ thức lượng trong tam giác vuông. Nó cho biết rằng trong một tam giác vuông, bình phương của độ dài cạnh huyền (cạnh đối diện góc vuông) bằng tổng của bình phương độ dài hai cạnh góc vuông.
Nếu
a, b là hai cạnh góc vuông và
c là cạnh huyền, thì:
c2= a2 + b2
Các tỉ lệ lượng giữa các cạnh và góc:
Sin, Cos, Tan (sinh, côs, tan): Là các tỉ số lượng tuyệt vời
>> Xem thêm: Công thức tính diện tích hình tròn
Tam giác vuông
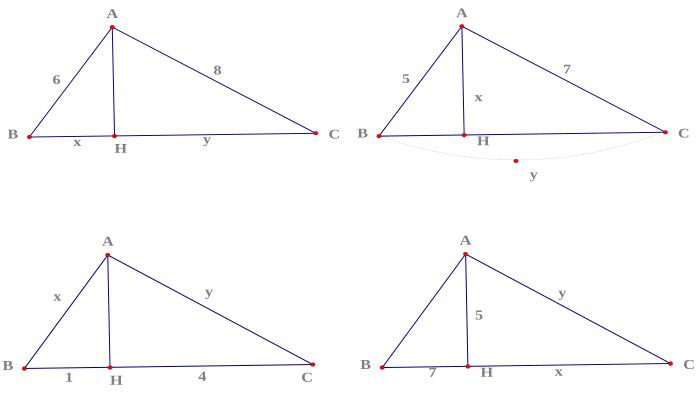
Trong toán học, hệ thức về cạnh và đường cao trong tam giác vuông là tập hợp các quy tắc quan trọng để tính toán các đại lượng liên quan đến các cạnh và đường cao của tam giác vuông. Đây là những công thức cơ bản và hữu ích trong lượng giác và hình học.
Cạnh và Đường Cao
Trong một tam giác vuông ABC có góc vuông tại A, cạnh huyền là c, và các cạnh góc vuông là a và b:
Cạnh huyền (c): Là cạnh đối diện với góc vuông và là cạnh dài nhất trong tam giác vuông.
Cạnh góc vuông (a và b): Là hai cạnh còn lại của tam giác vuông.
Đường cao từ góc vuông (h): Là đoạn thẳng kết nối đỉnh góc vuông với đáy đối diện sao cho vuông góc với đáy.

Học sinh trong giờ toán
Hệ Thức về Cạnh và Đường Cao
Đường cao và cạnh huyền:
h=ab/c
Trong đó:
h là độ dài đường cao từ góc vuông xuống cạnh huyền.
a và b là độ dài hai cạnh góc vuông.
c là độ dài cạnh huyền.
Cạnh góc vuông và đường cao:
a=ch/b
b=ch/a
Ứng Dụng Của Hệ Thức về Cạnh và Đường Cao
Hệ thức về cạnh và đường cao trong tam giác vuông cung cấp những công cụ cơ bản để tính toán các giá trị hình học quan trọng như độ dài cạnh và đường cao. Những công thức này không chỉ giúp hiểu rõ hơn về các mối quan hệ hình học trong tam giác vuông mà còn có thể áp dụng vào các bài toán thực tế trong các lĩnh vực như xây dựng, thiết kế, vật lý, và các ngành khoa học khác.

Ứng dụng của toán học vào đời sống
Trong toán học và lượng giác, tỉ số lượng giác của góc nhọn là các tỉ số giữa các độ dài các cạnh trong một tam giác vuông. Các tỉ số này là các hàm lượng giác của một góc và thường được ký hiệu bằng các từ viết tắt: sin, cos, tan, cot, sec và cosec. Các tỉ số này có vai trò quan trọng trong việc tính toán và phân tích các mối quan hệ hình học trong các tam giác vuông.
Các Tỉ Số Lượng Giác Chính
Trong một tam giác vuông ABC có góc vuông tại A và các cạnh a, b, c (với c là cạnh huyền):
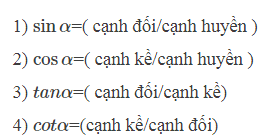
Ứng Dụng Của Tỉ Số Lượng Giác
Tỉ số lượng giác của góc nhọn có nhiều ứng dụng trong thực tế, đặc biệt là trong các lĩnh vực liên quan đến xử lý hình ảnh, thiết kế đồ họa, vật lý, kỹ thuật, và khoa học máy tính. Chúng giúp xác định các tỉ lệ quan trọng giữa các đại lượng hình học và là công cụ quan trọng trong tính toán và mô hình hóa các hiện tượng trong thế giới thực.